この記事はRetty Advent Calendar 2019 - Qiita 17日目の記事です。
昨日はimaizumeさんのXcode 11でビルドしたRetty iOSアプリの検索バーが突然反応しなくなった訳でした
はじめに
はじめまして! Rettyのデータアナリストの二見です Rettyの中でもWebやアプリなどのプロダクト側の分析を担当しています。入社して半年ほどなのですが、普段の分析の様子などは以下の記事にまとまっているのでもしよろしければご覧ください。
さて今回の記事では重回帰分析を取り上げたいと思います。聞いたこともある方も多いかと思いますが、実際のプロダクトのデータで利用すると結構複雑です。
この記事では回帰分析の概念から入って、実際の分析でどのように利用できるかまでをまとめています。
<注意1:この記事では一般線形回帰を軸にまとめています>
<注意2:本記事中で紹介されているデータ・図表は説明のためのサンプルです>
- はじめに
- 傾向把握しやすい回帰分析
- 重回帰分析とは?
- 実プロダクトで重回帰分析を利用する際の注意点
- BigQuery + statsmodels + scikit-learnで行う重回帰分析
- Rettyにおける回帰分析
傾向把握しやすい回帰分析
プロダクトを運用していると様々な場面でデータ分析を行います。SQLからデータを出してクロス集計を行なったり、施策の効果検証に検定を行なったり、様々な分析手法を駆使してプロダクトのグロースを測ります。
その中でプロダクトの今後の方向性やKPIを達成していくための狙い目の特定に関して回帰分析は役に立ちます。
例えば、月間の口コミ投稿数とサービスへの訪問数の散布図を書きます

この時の相関係数(月間の口コミ投稿数とサービスへの訪問数)は0.8とします。つまり月間で多く口コミを投稿してくれているユーザーさんは、たくさんサービスを利用してくれている傾向にあると言えます。当たり前の結果になりました。
これを初めて訪れたユーザーさん(新規)と、継続してサービスを使っているユーザーさんに分けて表示してみると以下のようになりました。

上記のような散布図になった時、月間の口コミ投稿数を増やすには新規をユーザーさんを増やす施策を打った方がいいのか、既存のユーザーさんに継続してもらう方がいいのかぱっと見ではわかりません。
もちろん新規と既存の軸だけであればそれぞれの相関係数から判断しても良いように思えますが、前提条件を揃えないと間違った意思決定や結論を導くことになりかねません。
この問いに対して定量的に式化していくことができるのが回帰分析になります。
重回帰分析とは?
回帰分析の中でも複数の変数を同時に評価できるのが重回帰分析です。重回帰分析の形は以下のように表すことができます。
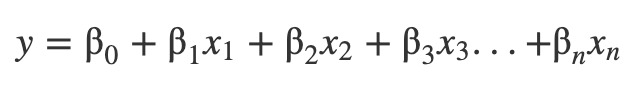
この時のを目的変数、
を説明変数と呼びます。この説明変数が単体のものを単回帰分析と呼びます。
先ほどの例だと月間の口コミ投稿数が目的変数、月間の訪問回数と新規かどうかが説明変数となります。

重回帰分析は他の説明変数を固定した時に、該当の説明変数を動かすとどれくらい目的変数を動かせるかを表しています。 上記の式からは以下のことがわかります。
月間訪問回数が全く同じだった場合、新規のユーザーさんを1人増やすとどれくらい口コミ数が増えるか
実プロダクトで重回帰分析を利用する際の注意点
実際にプロダクトのデータを使って重回帰分析を行う場合には、いくつかの注意点があります。
プロダクトのデータはばらつきも大きく、RettyのようなtoC向けであれば季節性のトレンド影響をもろに受けます。データの前処理を行うか、前提条件をしっかり把握した上で基準として利用する必要があります。
季節性や施策の打ちやすさ

気をつけなければならない点として、各説明変数の特性を前提におかなければなりません。実際のプロダクトでは季節によって作った重回帰モデルの値が変化したり、結果として施策の打ちづらい変数ばかりが残ることもあります。
Rettyはグルメサービスということもあり、忘年会や年末の飲み会に向けて季節性がかなり強くでます。この辺りのプロダクト特有の性質であったり、ドメイン知識は念頭に置きながら変数の説明をする必要があります。
交互作用と多重共線性
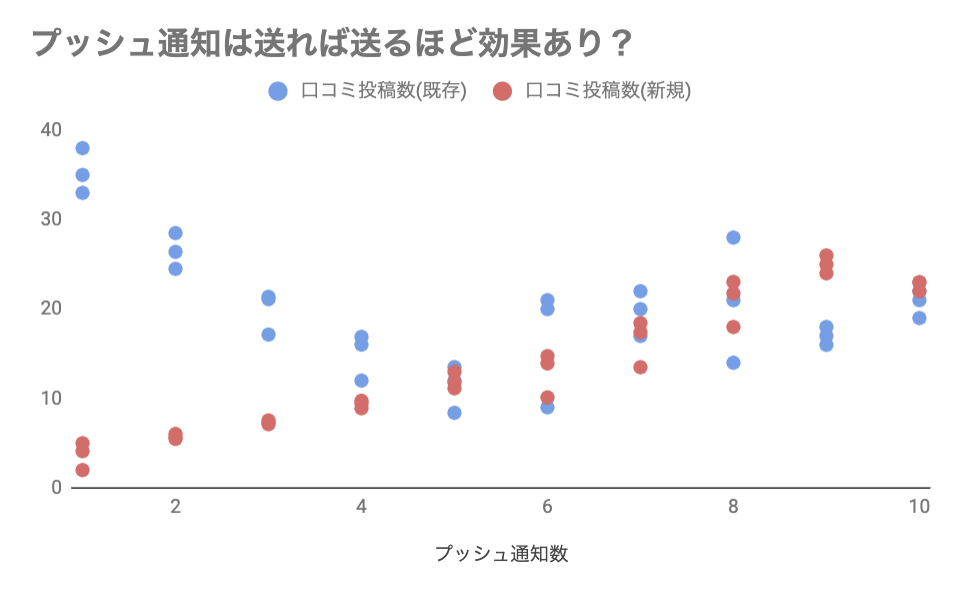
上記の散布図は月間の口コミ投稿数とプッシュ通知数による相関を表しています。既存と新規のユーザー別で見ると、一概にプッシュ通知を送る施策を打てば良いと言いづらそうです。
重回帰分析を行う際もこの新規と既存の前提条件を揃えないとプッシュ通知を送る施策自体に効果がないと意思決定する恐れがります。このように前提条件を揃えて初めて相関が現れるものを交互作用と言います。
またPVとUUのように独立変数間に強い相関があるものは多重共線性と呼び、正確な重回帰分析に影響することがあります。説明変数を選ぶ際はこのように前提条件が揃っているか、多重共線性がないかを確認してから行う必要があります。
ここまで変数選択の前提を考えて、実際に重回帰分析にかけてみます。
BigQuery + statsmodels + scikit-learnで行う重回帰分析
重回帰分析を行う方法は色々ありますが、今回はBigQueryから直接データを読み込んでstatsmodelsというライブラリを利用して重回帰分析を行いたいと思います。
また、作成したモデルの評価としてscikit-learnから交差検証とMAEを利用しています。scikit-learn単体でも重回帰分析を行うことはできますが、Pythonからだとp値を出す関数定義をしなければならないなどのデメリットもあるため両方利用しています。

最近ではSQLから簡易に重回帰分析を行うBigQuery MLもありますが、作成したモデルの評価がしづらかったり、変数それぞれのp値を出すことができなかったりするので今回は採用していません。
回帰モデルの作成
今回はBigQueryとGoogle Colabを連携して、重回帰分析を行います。
Google Colabを開いて、以下のモジュール実行からBigQueryと連携します。
from google.colab import auth auth.authenticate_user()
以下のようにしてGoogle ColabからBigQueryのSQLを叩けるようになります。
%%bigquery --project プロジェクト名 格納する変数 select * from `project.dataset.table` order by 1
SQLが実際に実行されて格納された変数に結果が格納されます。この結果を元に重回帰分析をかけていきます。
## statsmodelsをimport import statsmodels.api as sm import statsmodels.formula.api as smf ## sklearnをimport from sklearn.model_selection import train_test_split ## 検証用のデータセットに分割 from sklearn.model_selection import cross_val_score ## 検証用のデータセットを作成 from sklearn.linear_model import LinearRegression ## 線形回帰用 import sklearn.model_selection ## モデルの評価に関して ## MAEを計測するためのモジュール from sklearn.metrics import mean_absolute_error ## 基本的なモジュールを追加 import pandas as pd import numpy as np df.fillna(0) ## Nullに一律で0を入れる ## 説明変数を入れる X=df[[ "n_visit_monthly" , "is_new" , "n_push_notification"]] ## 目的変数を入れる Y=df['n_post_monthly'] # 交差検証用の分割 X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X,Y) model_lreg = LinearRegression() model_lreg.fit(X_train, Y_train) # statsmodelsを利用してモデル作成 X_stat = sm.add_constant(X) y_stat=Y # 最小二乗法でモデル化 model_stat = sm.OLS(y_stat, X_stat) result_stat = model_stat.fit() # 重回帰分析の結果を表示する result_stat.summary()
以上を実行すると以下のような結果を得ることができます。

説明変数それぞれが並んでおり、偏回帰係数や標準偏回帰係数が出力されます。実際の式に直すと以下のようになります。

標準偏回帰係数はそれぞれの説明変数の重要度を表しています。PVやUU、CVRなど目的変数に直接的に大きな影響を与える説明変数はこの標準偏回帰係数が大きくなる傾向にあります。
p値と95%信頼区間から影響度の大きい変数を特定する
重回帰分析を行うどの変数が大きく影響しているかを特定することができます。プロダクトの方向性や施策の方向性を意思決定していく上ではモデルの予測精度よりもこちらの変数の調整が重要になってくる可能性があります。
中でもp値と95%信頼区間から、算出された偏回帰係数が偶然によるものなのかがわかります。

p値はざっくり言うとそれぞれの偏回帰係数が偶然その値になったのかどうかを表しています。p値の基準は0.05ですので、0.05を上回るものは偶然のその傾向になっている可能性があります。また偏回帰係数がどの範囲で推移するのかは95%信頼区間を見るとわかります。
標準偏回帰係数とp値、95%信頼区間を見ることによって目的変数に対して影響度の大きい変数を特定することができます。
モデル評価と変数選択について
作成した重回帰分析が目的変数に対してどれくらい当てはまるかを評価する方法はいくつかあります。
# 交差検証用の分割
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X,Y)
model_lreg = LinearRegression()
model_lreg.fit(X_train, Y_train)
先ほど記述した上記は、交差検証と呼ばれる評価方法です。元データから検証用のデータを生成し、重回帰分析でどれくらい当てはまるかを表しています。分割したデータから当てはまりがどれくらいかを評価するのには以下のスクリプトを実行します。
print("決定係数(学習用):", new_lreg.score(X__train, Y__train)) print("決定係数(テスト用):", new_lreg.score(X__test, Y__test))
またMAE(Mean Absolute Error)と呼ばれる評価方法も存在し、重回帰分析から導出される目的変数が絶対値でどれくらいの差分があるかを表しています。MAEの式は省略しますが、以下のようにして評価することができます。
print("MAE:",mean_absolute_error(Y__train ,model_lreg.predict(X__train)))
MAEによって算出された値がビジネス的にどこまで許容できるかは意思決定者と相談して調整すると良いと思います。
また変数の選択にはステップワイズ法や増減法など様々な方法があります。pythonで直接これらの方法を試すには自ら関数を定義して行う必要があります。Rのパッケージからだとp値の算出や変数の選択を統計的に処理することができるので、Pyperなどを利用してRから統計処理を行うのもおすすめです。
Rettyにおける回帰分析

Rettyにおいて分析チームは意思決定にいかに貢献できたかがバリューとなります。上記の画像のようにドメイン理解が進んでいる状態であり、なおかつ課題の具体性が上がってくる場合はより複雑な分析手法に取り組んでいく余地があります。一方でより短い時間で意思決定にインパクトするものであれば簡易な集計で完了する場合が多いです。
出典:統計学が最強の学問である[実践編]
回帰分析の手法選択についてはアウトプットが量的であれば重回帰分析を用いて、質的であればロジスティック回帰を用います。
このようにプロダクトにおいて本当にその分析手法が妥当なものなのかどうかを判断しながら分析を進めることが大切になります。今回紹介した回帰分析はほんの入り口なので、興味のある方は統計的な手法から勉強してみても良いかもしれません!
それでは!
