この記事は、Retty Advent Calendar 2019 - Qiita10日目の記事です。
昨日は松田さんのCSSを10万行書いたフロントエンドエンジニアがコードレビューをする時に気をつけていることでした。
はじめに
こんにちは!Rettyのデータアナリストの飯田です。
いきなりですが、ネットワーク分析という手法をご存知でしょうか?
一言で言うと、「ある対象が行なった行為の意味を、その対象の属性からではなく、周りとの関係から明らかにしていこうとする試み」のことです。
本記事では、ネットワーク分析の手法を用いたコミュニティ構造の可視化についてご紹介したいと思います。
ネットワーク分析とは何か
ネットワーク分析は、グラフ理論から端を発した、ネットワークの性質を明らかにする分析手法で、分析対象は文字通りネットワーク(関係性)です。 ネットワークを表現する際には点と線でその関係性を表します。点のことをノード、線のことをエッジと呼びます。
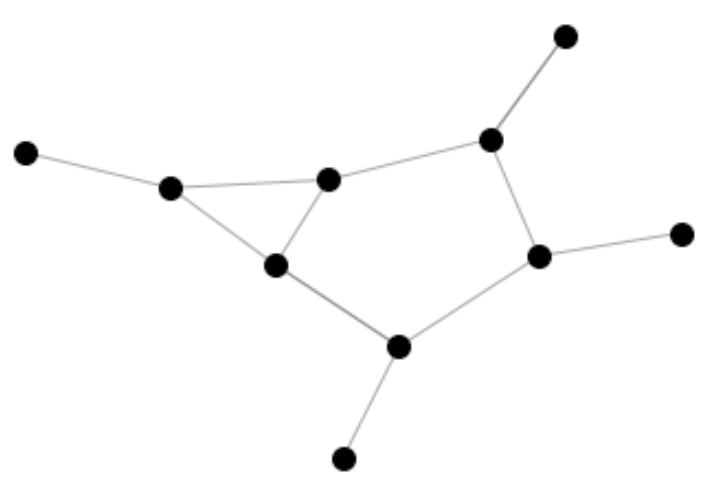
ネットワーク分析では、分析対象を理解する時にその対象の属性のみからではなく、他との関わりを持つ存在を同時に捉えて、その関係性の中で対象の行為の意味や思考を理解して行こうとします。 このネットワーク分析を用いることで、ネットワークの性質やそのネットワークの中での重要な点、ネットワーク内における分断リスクなどを明らかにすることができます。
これまで数多くのネットワークについての研究がされていて、有名どころだと論文の共著ネットワークやインターネットのウェブネットワーク、神経細胞のネットワーク構造などがあります。「六次の隔たり」や「弱いつながり」などの言葉もこの分野から出てきたものです。
ネットワーク分析の流れは、基本的に以下の3ステップになります。
- 関係定義
- 抽出と描画
- 特徴量の算出
以下では「Rettyのデータを用いたラーメン好きとカフェ好きのコミュニティ構造比較」をテーマに、各ステップに当てはめて行なっていきます。 今回はPython3.6とそのライブラリであるNetworkX 2.1を用いました。
コミュニティ構造比較
1. 関係定義
ネットワーク分析の最初のステップは、ノードとエッジの定義をすることです。「どんな条件の元に対象のノードが決まり、どんな関係性を持つノード同士を繋ぐのか」を定義していきます。
今回の事例の対象となるネットワークは、「ラーメン好きコミュニティ」と「カフェ好きコミュニティ」なので、以下の項目をそれぞれ定義する必要があります。 今回の事例の定義はそれぞれ「→」の後に記述しました。
①ノード
ノードとなる対象は何か
→東京都内のお店について投稿をしている一人一人のRettyユーザーさんラーメン(カフェ)好きをどう定義するか?
→ラーメン屋(カフェ)の累計投稿数30以上のユーザーさん
②エッジ
どんな状態のノード間にエッジを描くか?
→片方のユーザーさんがもう片方をフォローしている状態。有向グラフか無向グラフか?
→ネットワークは、向きを持つエッジで構成された有向グラフと、向きを持たないエッジで構成された無向グラフに分けることができるが、今回は単純化のため無向グラフを利用。エッジごとに重みをつけるか?
→単純化のためつけない。
2. 抽出と描画
このステップでは必要なデータセットを用意し、NetworkXとmatplotlibを用いて実際にネットワーク構造を視覚的に把握します。 NetworkXでネットワーク分析をする際には、以下の例のようなノードの配列とエッジの配列データをそれぞれ用意してあげる必要があります。
dataset = {
"nodes": [1,2,3]
, "edges": [(1,2), (2,3), (3,1)]
}
上記のデータセットを元に以下のコードで実際にネットワークを描画します。
import networkx as nx
import matplotlib.pyplot as plt
def draw_network(dataset):
G = nx.Graph(dataset["edges"])
pos = nx.spring_layout(G, k=0.5)
nx.draw_networkx_nodes(G, pos, nodelist=dataset["nodes"], node_color='black', node_size=50)
nx.draw_networkx_edges(G, pos, edgelist=dataset["edges"], edge_color='gray', alpha=0.7)
plt.axis('off')
plt.show()
draw_network(dataset)
3つのノードはそれぞれ全てのノードと結びついているため、以下のような三角形のネットワークを形成します。
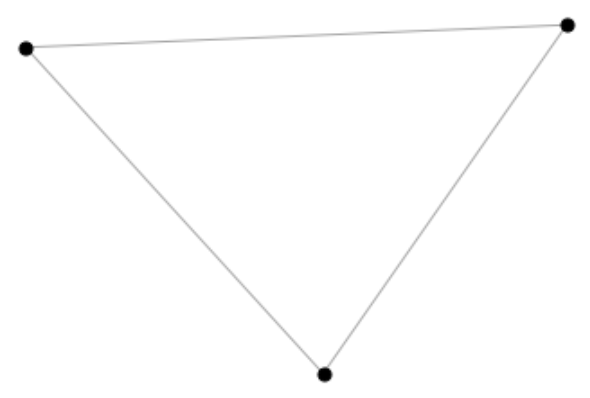
実際にラーメン、カフェ好きユーザーさん同士の繋がりネットワークの構造を見てみましょう。
①ラーメン
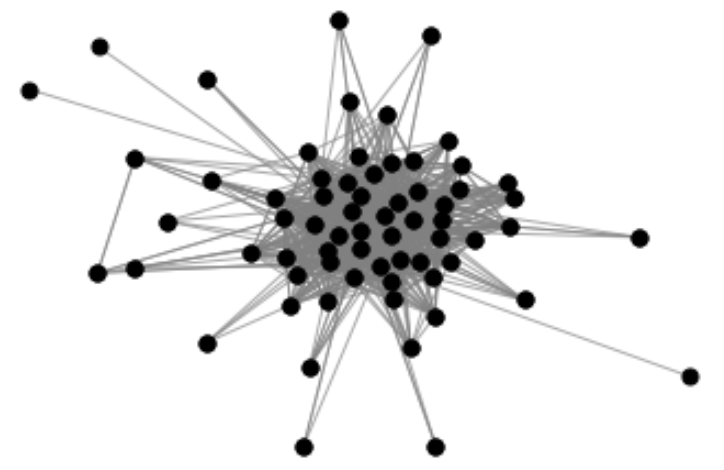
②カフェ

両コミュニティ共にユーザーさん同士でかなり繋がりを持っており、一部のユーザーさんがハブになっているというよりは、全体的にユーザーさん同士が繋がっていることが伺えます。
ただ、見た感じラーメン好きの方同士の方が、より繋がりが多いようにも見て取れます。カフェ好きコミュニティは繋がりの濃いユーザーさん同士が一部いるようですが、繋がりの少ないユーザーさんも一定数いそうです。
このように、ネットワーク構造の可視化は直感的にノード同士の繋がりを把握する上で非常に便利な手法です。しかし、コミュニティ同士を比較する際に「何がどれだけ違うのか」という点にまで深く切り込んで行けません。
3. 特徴量の算出
このステップでは、ネットワーク構造の特徴量を算出し、定量的にネットワーク同士を比較していきます。定量的な指標を用いることで、ネットワーク同士の比較をより客観的に行うことができるようになります。以下では、ネットワーク分析でよく用いられる3つの特徴量の説明をした後に、それぞれの値を算出していきます。
①クラスター係数
対象のネットワークがどれだけ密なのかを表す指標です。値は0から1を取り、1に近いほどネットワークの密度が高いことを意味します。
G = nx.Graph(dataset["edges"]) clustering_coefficient = nx.average_clustering(G) print(clustering_coefficient)
②平均経路長
平均経路長とは、ネットワークに含まれるノード全てのペアの最短経路長を平均した値のことです。この値が小さいほど直接繋がりを持たないノードとの距離が近いことを意味します。
G = nx.Graph(dataset["edges"]) average_shortest_path_length = nx.average_shortest_path_length(G) print(average_shortest_path_length)
③次数分布
次数分布とは、次数が全ノードの中で占める割合
を表した確率分布です。多くのネットワークで、この次数分布はべき分布に従うと言われています。
実際に算出した結果、それぞれ以下のようになりました。
| セグメント | ①クラスター係数 | ②平均経路長 |
|---|---|---|
| ラーメン | 0.68 | 1.71 |
| カフェ | 0.63 | 1.98 |
③次数分布
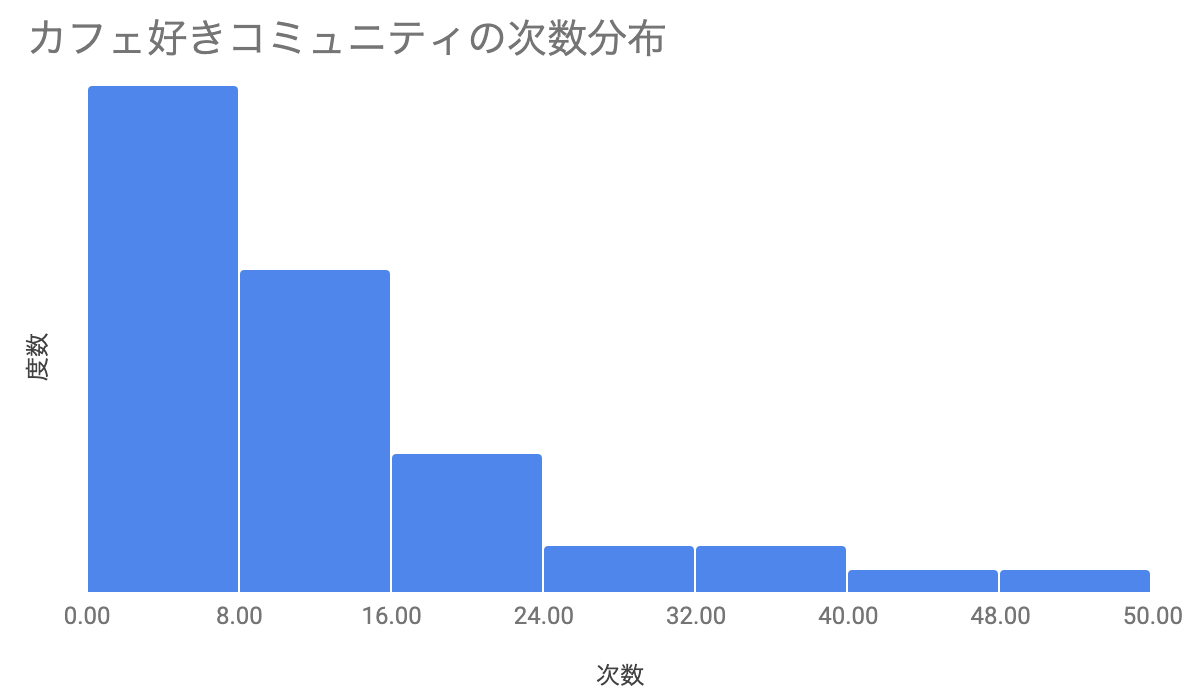
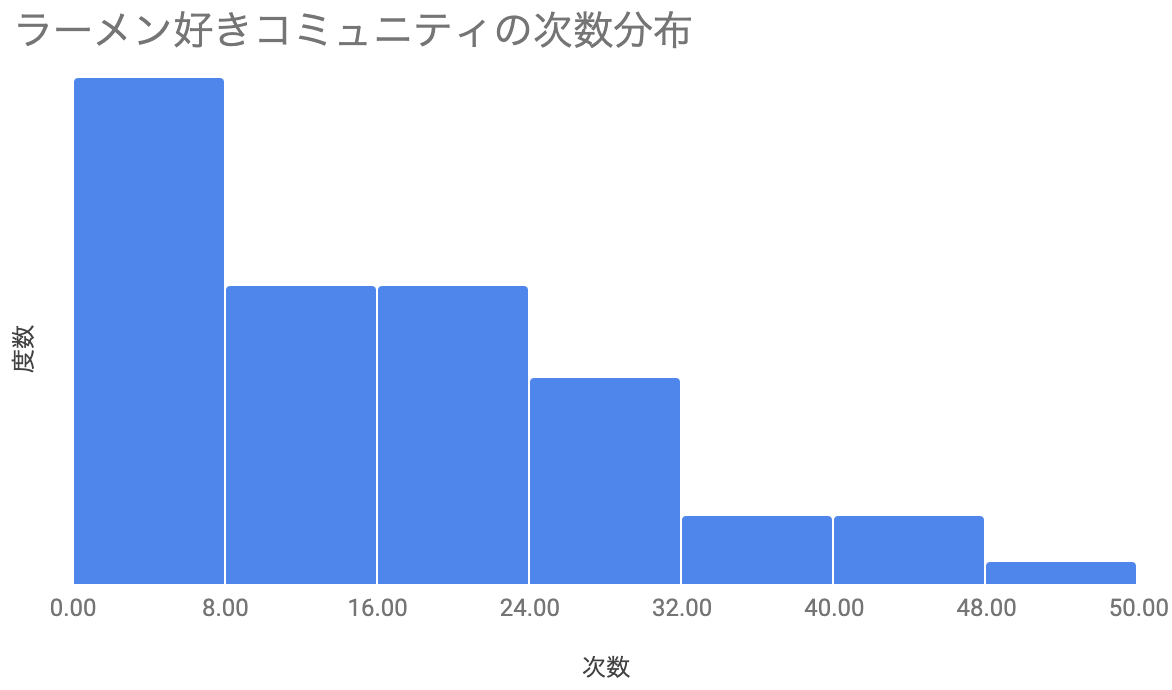
クラスター係数が高く平均経路長が短いことから、カフェ好きコミュニティよりもラーメン好きコミュニティの方が密度の濃いコミュニティであることが言えそうです。
また、次数分布からわかることとして、カフェ好きコミュニティの方が一部のユーザーさんに繋がりが比較的偏っている事がわかります。ネットワーク構造を視覚的に把握した際にも同様の傾向が見て取れた内容です。
以上様々な観点からコミュニティ構造の比較を行ってきましたが、カフェ好きよりもラーメン好きコミュニティの方が濃い繋がりを持っている事がわかりました。確かに私の周りにもカフェ好きよりもラーメンのほうが熱量高い方々がいるので、直感的にも納得感がある結果となりました。
おわりに
私がネットワーク分析に興味を持ったのは、「その人の行為はそれ自体の属性ではなく関係性の中で規定される」という考えが面白かったからです。 自分が今持っている考えや行動は自分自身の性格によるものもありますが、自分の身の回りにどんな人がいるのかに多分に影響を受けます。 普段あまり意識することはないですが、自分の最近の行動と身の回りの人たちとを見返してみると、思わぬ気付きがあるかもしれません。
少しでもネットワーク分析に興味を持った方がいらっしゃれば、以下の書籍は入門書として面白いのでぜひ読んでみてください!それでは!